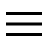La probabilidad acumulativa es una forma de medir la probabilidad de que un evento aleatorio ya haya ocurrido al menos una vez después de un cierto número de intentos, o rollos.
Contenido
- 1 ejemplo motivador
- 2 Función de probabilidad acumulada
- 3 ejemplos en Genshin Impact
- 3.1 Sistema de deseos
- 3.1.1 Incorporación de índices de lástima
- 3.1.2 Personajes de eventos
- 3.1.3 Personajes de Wanderlust
- 3.1.4 armas de evento
- 3.2 Jefes y dominios
- 3.1 Sistema de deseos
- 4 Propiedades de la función de probabilidad acumulada
- 5
Ejemplo motivador
Por ejemplo, después de lanzar un dado de 6 caras una vez, la probabilidad de que haya aparecido un 6 al menos una vez es ahora 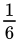 o 16.66%. Sin embargo, la probabilidad después de tirar por segunda vez es no
o 16.66%. Sin embargo, la probabilidad después de tirar por segunda vez es no 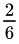 . Una buena forma de entender esto es imaginar 100 players cada uno con un dado de 6 lados. Después de una tirada, el número de players que han sacado al menos un 6 es aproximadamente el 17%, como se señaló anteriormente, así que saquemos a esos 17 jugadores del juego. Ahora solo 83 players permanecer. Una vez que salgan todos por segunda vez, esperamos que otro 16.66% de esos jugadores hayan sacado un 6, pero ahora que hay menos jugadores, el número que tenemos que eliminar también es menor, solo alrededor de 13. Del mismo modo, en en la tercera tirada solo esperamos que 11 o 12 nuevos jugadores obtengan un 6, en la cuarta tirada solo 9, 7 en la quinta tirada, y así sucesivamente. Mientras que la en total número de jugadores que han sacado al menos un seis aumentos cada ronda, con un total de 56.5% para la ronda 5, el número de Un nuevo jugadores que se unen a ese grupo en cada ronda disminuye de forma exponencial.
. Una buena forma de entender esto es imaginar 100 players cada uno con un dado de 6 lados. Después de una tirada, el número de players que han sacado al menos un 6 es aproximadamente el 17%, como se señaló anteriormente, así que saquemos a esos 17 jugadores del juego. Ahora solo 83 players permanecer. Una vez que salgan todos por segunda vez, esperamos que otro 16.66% de esos jugadores hayan sacado un 6, pero ahora que hay menos jugadores, el número que tenemos que eliminar también es menor, solo alrededor de 13. Del mismo modo, en en la tercera tirada solo esperamos que 11 o 12 nuevos jugadores obtengan un 6, en la cuarta tirada solo 9, 7 en la quinta tirada, y así sucesivamente. Mientras que la en total número de jugadores que han sacado al menos un seis aumentos cada ronda, con un total de 56.5% para la ronda 5, el número de Un nuevo jugadores que se unen a ese grupo en cada ronda disminuye de forma exponencial.
Específicamente, la probabilidad de sacar un 6 al menos una vez en x tiradas es 1 menos la probabilidad de no sacar un 6 en absoluto:
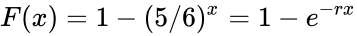
dónde  .
.
Función de probabilidad acumulada
Para expresar este fenómeno matemáticamente, podemos utilizar la siguiente fórmula: [1]

dónde 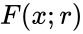 es la probabilidad acumulada que ya ha ocurrido un evento,
es la probabilidad acumulada que ya ha ocurrido un evento, 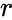 es la y en el que ocurre ese evento, y
es la y en el que ocurre ese evento, y 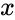 es la cantidad de rollos que han ocurrido hasta ahora. Las tiradas negativas no tienen sentido por definición, por lo que la función de probabilidad siempre es cero allí.
es la cantidad de rollos que han ocurrido hasta ahora. Las tiradas negativas no tienen sentido por definición, por lo que la función de probabilidad siempre es cero allí.
Para darle sentido a esta fórmula, es útil reorganizarla. La mayoría de las veces, nos interesa saber qué valor 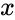 da una probabilidad acumulativa particular. Esto es útil porque nos dice cuántas tiradas se requieren antes de que sea probable que ocurra un evento. Es posible que deseemos saber cuántos rollos antes de que alcance el 50%, 90% o 99%, o cualquier otro valor arbitrario. La fórmula se puede reorganizar de la siguiente manera para darnos este resultado:
da una probabilidad acumulativa particular. Esto es útil porque nos dice cuántas tiradas se requieren antes de que sea probable que ocurra un evento. Es posible que deseemos saber cuántos rollos antes de que alcance el 50%, 90% o 99%, o cualquier otro valor arbitrario. La fórmula se puede reorganizar de la siguiente manera para darnos este resultado:
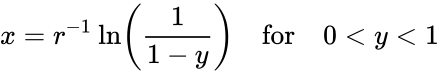
Dónde 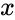 es el número de rollos necesarios para alcanzar
es el número de rollos necesarios para alcanzar 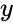 , que se puede considerar como un nivel de certeza de que un evento ya habrá ocurrido al menos una vez, expresado como una fracción de 1. Por lo tanto, para un
, que se puede considerar como un nivel de certeza de que un evento ya habrá ocurrido al menos una vez, expresado como una fracción de 1. Por lo tanto, para un 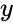 valor de 0.5, esperaría que si 100 personas "lanzaran un dado"
valor de 0.5, esperaría que si 100 personas "lanzaran un dado" 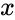 número de veces, 50 de ellos habrían encontrado el resultado que le interesa (el que tiene probabilidad
número de veces, 50 de ellos habrían encontrado el resultado que le interesa (el que tiene probabilidad 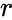 ) al menos una vez. Por ejemplo, el número de tiradas necesarias para obtener una cierta probabilidad acumulativa (algunas
) al menos una vez. Por ejemplo, el número de tiradas necesarias para obtener una cierta probabilidad acumulativa (algunas 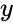 valor) al lanzar "uno" en algunos tamaños de dados comunes, como se encuentra usando esta fórmula, son los siguientes:
valor) al lanzar "uno" en algunos tamaños de dados comunes, como se encuentra usando esta fórmula, son los siguientes:
| Número de tiradas necesarias para obtener una probabilidad acumulada dada en varios tamaños diferentes de dados | ||||
|---|---|---|---|---|
| Tipo de dados | 50%
Probabilidad acumulativa (y = 0.5) |
90%
Probabilidad acumulativa (y = 0.9) |
99%
Probabilidad acumulativa (y = 0.99) |
Gráfico |
| Dados de 6 caras | 4.16 | 13.82 | 27.63 | 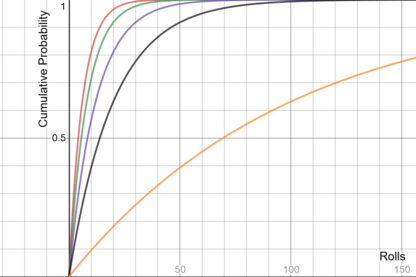 5 curvas, una para cada dado, que muestran su probabilidad acumulada a medida que aumenta el número de tiradas |
| Dados de 8 caras | 5.54 | 18.42 | 36.84 | |
| Dados de 10 caras | 6.93 | 23.03 | 46.05 | |
| Dados de 20 caras | 13.86 | 46.05 | 92.10 | |
| Dados de 100 caras | 69.31 | 230.26 | 460.52 | |
Ejemplos en Genshin Impact
Sistema de deseos
El sistema de deseos de Genshin Impact es una serie de eventos aleatorios, compuestos por numerosos resultados y cada uno tiene una probabilidad única de ocurrir cada vez que se pide un deseo. Esto significa que podemos aplicar el modelo matemático desarrollado anteriormente para determinar valores interesantes, como cuántos deseos se necesitarían antes de que el 50% de los jugadores obtengan un resultado determinado. Para hacer esto, primero analicemos lo que sucede cada vez que se pide un deseo. Primero, se determina la rareza del deseo, siendo 5 *, 4 * o 3 *. Una vez que se ha determinado la rareza, se selecciona uno de los elementos de la tabla de botín especificada, y ese elemento es el resultado final del deseo. Para determinar la tasa de un elemento específico dentro de una tabla, solo necesitamos dividir la tasa a la que aparece la tabla por el número de elementos en esa tabla. Para obtener un tratamiento más detallado de las tasas de artículos en niveles de rareza específicos en todos los diferentes banners de deseos, consulte la página sobre probabilidades de deseos ampliadas.
| Asunto
(Deseo estándar) |
Tasa básica
(Cualquier personaje o arma) |
Tamaño de la piscina | Tarifa de artículo único
(Personaje específico o arma) |
|---|---|---|---|
| Personaje de 5 estrellas | 0.3% | 5 | 0.04% |
| Arma de 5 estrellas | 0.3% | 10 | 0.02% |
| Personaje de 4 estrellas | 2.6% | 18 | 0.14% |
| Arma de 4 estrellas | 2.6% | 18 | 0.14% |
| Arma de 3 estrellas | 94.3% | 13 | 7.254% |
Usando estas tasas, podemos determinar cuántos rollos se requieren para alcanzar una cierta probabilidad acumulativa de haber adquirido un determinado artículo al menos una vez.
Incorporación de tasas de lástima
Sin embargo, las tarifas base para artículos de cuatro y cinco estrellas en realidad no cuentan la historia completa. Las tasas de lástima, o garantías, pueden afectar el cálculo de manera dramática. Esencialmente, hacen que la función de probabilidad acumulativa discontinuo cambiando la velocidad a la que aparecen los elementos periódicamente, siempre que no se haya invocado ningún elemento del nivel especificado después de suficientes tiradas. Hay varias formas de compensar esto. En el juego, una segunda tasa, llamada Tasa promedio, incluidas garantías, se muestra junto a la tarifa base. Se podría reemplazar la tasa base con esta tasa promedio ajustada y los resultados serían más precisos. El enfoque más preciso sería utilizar la tasa base, pero segmentar la función en los intervalos en los que ocurren las tasas de lástima. Sin embargo, esto tiene el resultado indeseable de requerir más cálculos y crear una función discontinua. También pierde algo de precisión cuando se trabaja con probabilidades de subcategoría, ya que una parte de los jugadores que alcanzan el umbral de la tasa de lástima ya habrán invocado un elemento del nivel deseado, por lo que el contador de lástima quedará inactivo, pero no el elemento deseado; y no es trivial agregar pasos de lástima discontinuos en cada tirada subsiguiente para estimar cuándo podría haberse reiniciado el contador. Por lo tanto, no es posible una solución analítica pura; solo puede calcular analíticamente un límite superior o inferior aproximado.
El resultado más deseable sería una simulación computacional completa que luego podría compararse con los diversos métodos analíticos.
Personajes del evento
Personaje de evento promocional de 5 estrellas
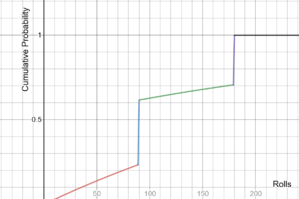
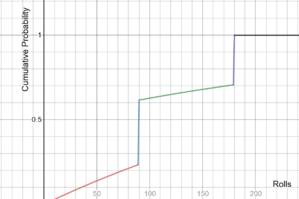
Las posibilidades de haber convocado ya al personaje de banner 5 *. Tenga en cuenta que esta solución analítica asume que todos los que reciben una citación por lástima la reciben en la convocatoria 90 o 180, lo que puede no ser cierto en la práctica.
Para un personaje de evento promocional de 5 estrellas, la tasa base es 0.3% (tasa base de cinco estrellas dividida por dos, ya que hay un 50% de probabilidad de convocar al personaje de evento de 5 estrellas cada vez que ocurre una convocatoria de 5 estrellas). También hay una mecánica de lástima, de modo que si no se ha producido una invocación de 5 estrellas dentro de las 89 invocaciones, se garantiza que la siguiente invocación será una invocación de 5 estrellas. Combinadas, estas dos mecánicas de lástima garantizan que, como máximo, se requieran 180 deseos para convocar a un personaje promocional de 5 estrellas. Una solución analítica que ignora la mecánica de la primera lástima (la garantía) se puede ver en el siguiente gráfico.
La razón por la que esta solución analítica ignora la garantía es que cambia la velocidad a la que ocurren los eventos (del 0.3% del tiempo, la mitad de los 5 * tirones, al 0.6% del tiempo, el 100% de los 5 * tirones). La forma en que esto afecta la tasa a la que ocurren los eventos en la práctica no es trivial: es obvio que en el primer lanzamiento, la tasa será del 0.3% para todos, y que para el 90 °, la tasa será del 0.6% para todos los jugadores restantes. Sin embargo, para determinar cómo cambia la tasa promedio en los primeros 89 rollos, sería necesario resolver una ecuación diferencial. Sin embargo, podemos evitarlo por completo y obtener un resultado más preciso realizando una simulación.
Como se ha explicado, la mecánica de la lástima hace que sea muy difícil encontrar una solución analítica significativa a nuestro problema. Para superar esto, podemos realizar una simulación de una gran cantidad de rollos y analizar los resultados empíricamente o compararlos con nuestra solución analítica. Porque el número devuelto por la función de probabilidad acumulada 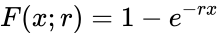 representa el porcentaje de una población determinada que esperamos haber experimentado un resultado al menos una vez después
representa el porcentaje de una población determinada que esperamos haber experimentado un resultado al menos una vez después 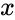 número de tiradas, podemos simular los resultados de esta función tomando una gran "población" de individuos simulados y tirando con cada uno hasta que alcancen el resultado deseado o el número máximo de tiradas. Luego sumamos la cantidad de personas que alcanzaron el resultado en cualquier paso dado a las que ya alcanzaron el resultado, creando una curva que muestra cuándo cada miembro de nuestra población alcanzó el resultado deseado. A continuación puede ver las curvas respectivas de dos de estas simulaciones, una con diez mil individuos simulados y la otra con cien.
número de tiradas, podemos simular los resultados de esta función tomando una gran "población" de individuos simulados y tirando con cada uno hasta que alcancen el resultado deseado o el número máximo de tiradas. Luego sumamos la cantidad de personas que alcanzaron el resultado en cualquier paso dado a las que ya alcanzaron el resultado, creando una curva que muestra cuándo cada miembro de nuestra población alcanzó el resultado deseado. A continuación puede ver las curvas respectivas de dos de estas simulaciones, una con diez mil individuos simulados y la otra con cien.
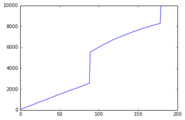
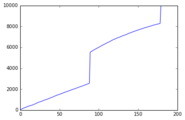 Esta simulación contenía 10 000 "individuos". Cada uno lanzó números aleatorios hasta obtener el carácter de banner de 5 *, teniendo en cuenta tanto la garantía de que el segundo 5 * extraído será el personaje de banner, como la regla de lástima de los 90 rollos.
Esta simulación contenía 10 000 "individuos". Cada uno lanzó números aleatorios hasta obtener el carácter de banner de 5 *, teniendo en cuenta tanto la garantía de que el segundo 5 * extraído será el personaje de banner, como la regla de lástima de los 90 rollos.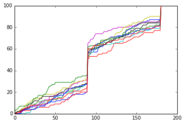
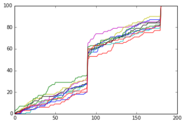 Este gráfico muestra la misma información, pero para diez corridas de solo 100 individuos simulados. Aquí, las curvas son visiblemente irregulares y cada una es sustancialmente diferente de la anterior, ya que la naturaleza aleatoria de la simulación no se ha "extendido" en tantas muestras.
Este gráfico muestra la misma información, pero para diez corridas de solo 100 individuos simulados. Aquí, las curvas son visiblemente irregulares y cada una es sustancialmente diferente de la anterior, ya que la naturaleza aleatoria de la simulación no se ha "extendido" en tantas muestras.
La gran conclusión de estas simulaciones es la siguiente:
- La solución analítica es una subestimación la mayor parte del tiempo, mostrando que casi el 30% de la población alcanza la segunda lástima, mientras que las simulaciones muestran que solo alrededor del 20% de los individuos simulados llegarán hasta el 180o deseo / tirada sin tener recibió el carácter de banner de 5 * al menos una vez. Esto sucede principalmente porque no tenemos en cuenta el cambio en la tasa, del 0.3% al 0.6%.
- La solución analítica muestra que una mayor parte de la población recibe su lástima en el 90º rollo (cerca del 60%) que en realidad (más cerca del 55% en las simulaciones). Este es el único caso de una sobreestimación en la solución analítica, y sucede porque no contabilizamos a las personas que pueden haber recibido un 5 * (pero no el carácter de banner) en algún momento entre el 1er y el 90º rollo, y por lo tanto no son elegibles para la compasión en el 90º rollo. Verá, sin embargo, que la curva en las simulaciones aumenta mucho más rápidamente después de la tirada 90, porque estos individuos están recibiendo su propia lástima un poco más tarde que los demás.
- Incluso en un entorno de simulación, todavía hay grandes picos en los deseos 90 y 180. Esto se debe a que grandes porciones de la población simulada están activando la mecánica de la lástima; La lástima, que se dispara después de 90 deseos infructuosos, ocurre cuando esperamos que solo alrededor del 30% de la población haya convocado 5 *. Esto significa que cuando un jugador llega hasta el final de la lástima, no tiene "mala suerte" si definimos tener suerte como alcanzar el resultado deseado antes del 50% de los demás participantes en una población determinada. Alrededor de dos tercios de los jugadores siempre sentirán lástima. Esto es lo que hace que el Tasa promedio, incluidas garantías, engañoso. Si bien esta tasa es el promedio sobre un gran número de tiradas, si implementas una regla de parada (un jugador deja de tirar después de obtener el artículo deseado), la tasa real siempre es menor (porque, a menos que termines con una tirada de lástima, habrá Sea siempre alguna lástima que no llegaste).
- En particular, aproximadamente el 20% de la población no recibirá el personaje de banner 5 * hasta el lanzamiento 180. Esto significa que si te comprometes a rodar hasta que obtengas un determinado personaje de estandarte, tienes una probabilidad entre cinco de "llegar hasta el final" a la segunda lástima. De manera similar, hay una probabilidad de una entre cinco de que coloques al personaje entre las tiradas 1 y 89; y de las tres quintas partes restantes del tiempo, tirarás del personaje ya sea en la primera lástima, o entre las tiradas 91 y 179, dividido en partes iguales.
Personaje de evento promocional de 4 estrellas
Resolver las densidades de probabilidad para los caracteres de 4 estrellas es, en general, más complicado que los caracteres de 5 estrellas. Esto se debe a que el grupo de personajes es más grande, siempre hay armas en el grupo y no hay garantía de obtener algún personaje de 4 estrellas en particular. Sin embargo, para resolver la probabilidad acumulada de obtener al menos uno de cualquier carácter de evento de 4 estrellas, el proceso es el mismo que para el carácter de evento de 5 estrellas, pero con diferentes tasas en las fórmulas. Entonces, esta información es relativamente fácil de obtener (solo necesitamos repetir los pasos anteriores). En el caso de los personajes de 4 estrellas, también es más probable que nos interese saber cuántos de ellos es probable que obtengamos en una cantidad fija de deseos, normalmente 90 o 180; porque, en el contexto de obtener un personaje 5 *, son recompensas extra. Entonces, examinaremos este problema también.
Cualquier personaje de evento de 4 estrellas
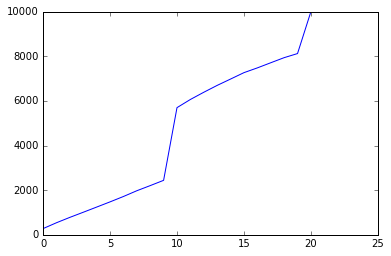
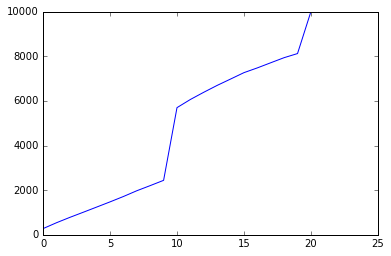
Esta es una simulación, con n = 10 000, de personas que se enrollan en el banner del evento y que han recibido al menos un carácter de banner de 4 *.
Si no nos preocupa obtener un personaje de 4 estrellas en particular, las matemáticas son mucho más simples. Si estamos interesados en cuántos deseos se necesitarán para obtener al menos un personaje de 4 estrellas, las fórmulas son las mismas que para el personaje de 5 estrellas, pero las tarifas son ligeramente diferentes. A la derecha hay un gráfico de una simulación con 10 000 individuos, con las tarifas y el contador de lástima ajustados para reflejar los personajes de 4 estrellas.
Como era de esperar, la curva es muy similar a la curva del personaje del evento de 5 estrellas, pero en un número mucho menor de deseos. Sin embargo, los cortes de lástima ocurren en porcentajes de población muy similares, lo que no es un resultado trivial; esto indica que las tasas y los recuentos de lástima se eligieron intencionalmente para cortar al mismo porcentaje esperado de la población (alrededor del 30%) para los artículos de 5 y 4 estrellas.
Un personaje de evento de 4 estrellas en particular
Personajes de Wanderlust
Armas de eventos
Jefes y dominios
Propiedades de la función de probabilidad acumulada
Convergencia independiente de la tasa
La suerte y la falacia del jugador
Relación con la monetización
- ↑ https: //en.web pagepedia.org/web page / Cumulative_distribution_function # Ejemplos
Probabilidad acumulativa
(y = 0.5)
90%Probabilidad acumulativa
(y = 0.9)
99%Probabilidad acumulativa
(y = 0.99)
Gráfico de dados de 6 caras 4.16 13.82 27.63
5 curvas, una para cada dado, que muestran su probabilidad acumulada a medida que aumenta el número de tiradas