La probabilità cumulativa è un modo per misurare la probabilità che un evento casuale si sia già verificato almeno una volta dopo un certo numero di tentativi, o rotoli.
Contenuti
- 1 Esempio Motivante
- 2 Funzione di probabilità cumulativa
- 3 esempi nell'impatto di Genshin
- 3.1 Sistema dei desideri
- 3.1.1 Incorporazione dei tassi di pietà
- 3.1.2 Personaggi Evento
- 3.1.2.1 Personaggio evento promozionale a 5 stelle
- 3.1.2.2 Personaggio evento promozionale a 4 stelle
- 3.1.2.2.1 Qualsiasi personaggio evento a 4 stelle
- 3.1.2.2.2 Un particolare personaggio evento a 4 stelle
- 3.1.3 Personaggi della voglia di viaggiare
- 3.1.4 armi evento
- 3.2 Boss e Domini
- 3.1 Sistema dei desideri
- 4 Proprietà della funzione di probabilità cumulativa
- 5
Esempio motivante
Ad esempio, dopo aver lanciato una volta un dado a 6 facce, la probabilità che un 6 sia apparso almeno una volta è adesso 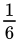 o 16.66%. Tuttavia, la probabilità dopo aver lanciato una seconda volta è non
o 16.66%. Tuttavia, la probabilità dopo aver lanciato una seconda volta è non 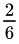 . Un buon modo per capirlo è immaginare 100 giocatori ciascuno con un dado a 6 facce. Dopo un tiro, il numero di giocatori che hanno ottenuto almeno un 6 è circa il 17%, come notato sopra, quindi eliminiamo dal gioco quei 17 giocatori. Ora solo 83 giocatori rimanere. Una volta che tutti avranno tirato una seconda volta, ci aspettiamo che un altro 16.66% di quei giocatori avrà tirato un 6 — ma, ora che ci sono meno giocatori, anche il numero che dobbiamo rimuovere è più piccolo, a solo circa 13. Allo stesso modo a al terzo tiro ci aspettiamo che solo 11 o 12 nuovi giocatori ottengano un 6, al quarto solo 9, 7 al quinto e così via. Mentre il totale numero di giocatori che hanno tirato almeno un sei aumenta ogni round, per un totale del 56.5% per round 5, il numero di nuovi giocatori che si uniscono a quel gruppo ad ogni round diminuisce in modo esponenziale.
. Un buon modo per capirlo è immaginare 100 giocatori ciascuno con un dado a 6 facce. Dopo un tiro, il numero di giocatori che hanno ottenuto almeno un 6 è circa il 17%, come notato sopra, quindi eliminiamo dal gioco quei 17 giocatori. Ora solo 83 giocatori rimanere. Una volta che tutti avranno tirato una seconda volta, ci aspettiamo che un altro 16.66% di quei giocatori avrà tirato un 6 — ma, ora che ci sono meno giocatori, anche il numero che dobbiamo rimuovere è più piccolo, a solo circa 13. Allo stesso modo a al terzo tiro ci aspettiamo che solo 11 o 12 nuovi giocatori ottengano un 6, al quarto solo 9, 7 al quinto e così via. Mentre il totale numero di giocatori che hanno tirato almeno un sei aumenta ogni round, per un totale del 56.5% per round 5, il numero di nuovi giocatori che si uniscono a quel gruppo ad ogni round diminuisce in modo esponenziale.
Nello specifico, la probabilità di ottenere un 6 almeno una volta in x tiri è 1 meno la probabilità di non ottenere affatto un 6:
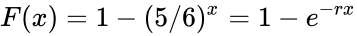
where  .
.
Funzione di probabilità cumulativa
Per esprimere matematicamente questo fenomeno, possiamo usare la seguente formula:[1]

where 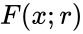 Europe è probabilità cumulativa che un evento si è già verificato,
Europe è probabilità cumulativa che un evento si è già verificato, 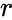 Europe è tasso in cui si verifica tale evento, e
Europe è tasso in cui si verifica tale evento, e 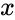 è il numero di rotoli che si sono verificati finora. I tiri negativi sono privi di significato per definizione, quindi la funzione di probabilità è sempre zero lì.
è il numero di rotoli che si sono verificati finora. I tiri negativi sono privi di significato per definizione, quindi la funzione di probabilità è sempre zero lì.
Per dare un senso a questa formula, è utile riordinarla. Il più delle volte, siamo interessati a sapere quale valore 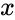 dà una particolare probabilità cumulativa. Questo è utile in quanto ci dice quanti tiri sono necessari prima che si verifichi un evento. Potremmo voler sapere quanti lanci prima che raggiunga il 50%, 90% o 99% o qualsiasi altro valore arbitrario. La formula può essere riorganizzata come segue per darci questo risultato:
dà una particolare probabilità cumulativa. Questo è utile in quanto ci dice quanti tiri sono necessari prima che si verifichi un evento. Potremmo voler sapere quanti lanci prima che raggiunga il 50%, 90% o 99% o qualsiasi altro valore arbitrario. La formula può essere riorganizzata come segue per darci questo risultato:
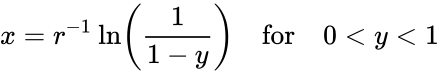
Dove 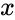 è il numero di rulli necessari per raggiungere
è il numero di rulli necessari per raggiungere 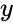 , che può essere pensato come un livello di certezza che un evento sarà già accaduto almeno una volta, espresso come una frazione di 1. Quindi, per un
, che può essere pensato come un livello di certezza che un evento sarà già accaduto almeno una volta, espresso come una frazione di 1. Quindi, per un 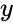 valore di 0.5, ti aspetteresti che se 100 persone "lanciassero un dado"
valore di 0.5, ti aspetteresti che se 100 persone "lanciassero un dado" 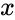 numero di volte, 50 di loro avrebbero incontrato il risultato che ti interessa (quello con probabilità
numero di volte, 50 di loro avrebbero incontrato il risultato che ti interessa (quello con probabilità 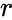 ) almeno una volta. Ad esempio, il numero di lanci necessari per ottenere una certa possibilità cumulativa (alcuni dati
) almeno una volta. Ad esempio, il numero di lanci necessari per ottenere una certa possibilità cumulativa (alcuni dati 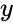 valore) tirando "uno" su alcune dimensioni di dadi comuni, come trovate usando questa formula, sono le seguenti:
valore) tirando "uno" su alcune dimensioni di dadi comuni, come trovate usando questa formula, sono le seguenti:
| Numero di lanci necessari per ottenere una data probabilità cumulativa su diverse dimensioni di dadi | ||||
|---|---|---|---|---|
| Tipo di dadi | 50%
Possibilità cumulativa (y = 0.5) |
90%
Possibilità cumulativa (y = 0.9) |
99%
Possibilità cumulativa (y = 0.99) |
Grafico |
| Dadi a 6 facce | 4.16 | 13.82 | 27.63 | 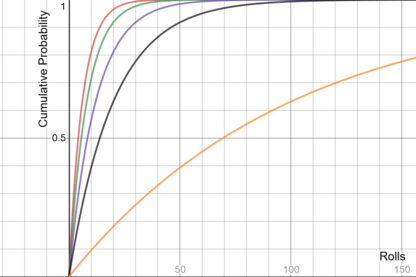 5 curve, una per ogni dado, che mostrano la loro probabilità cumulativa all'aumentare del numero di lanci |
| Dadi a 8 facce | 5.54 | 18.42 | 36.84 | |
| Dadi a 10 facce | 6.93 | 23.03 | 46.05 | |
| Dadi a 20 facce | 13.86 | 46.05 | 92.10 | |
| Dadi a 100 facce | 69.31 | 230.26 | 460.52 | |
Esempi nell'impatto di Genshin
Sistema dei desideri
Il sistema dei desideri di Genshin Impact è una serie di eventi casuali, composti da numerosi risultati che hanno ciascuno una probabilità unica di verificarsi ogni volta che viene espresso un desiderio. Ciò significa che possiamo applicare il modello matematico sviluppato sopra per determinare valori interessanti, come quanti desideri ci vorrebbe prima che il 50% dei giocatori ottenga un determinato risultato. Per fare ciò, analizziamo prima cosa succede ogni volta che viene espresso un desiderio. Innanzitutto, viene determinata la rarità del desiderio: 5*, 4* o 3*. Una volta determinata la rarità, viene selezionato uno degli oggetti dalla tabella del bottino specificata e quell'oggetto è il risultato finale del desiderio. Per determinare la velocità di un elemento specifico all'interno di una tabella, è sufficiente dividere la velocità con cui la tabella appare per il numero di elementi in quella tabella. Per una trattazione più dettagliata delle tariffe degli oggetti in specifici livelli di rarità in tutti i diversi banner dei desideri, consulta la pagina sulle probabilità espanse dei desideri.
| Articolo
(Desiderio standard) |
Tasso base
(Qualsiasi personaggio o arma) |
Dimensioni della piscina | Tariffa articolo unica
(personaggio o arma specifici) |
|---|---|---|---|
| Personaggio a 5 stelle | 0.3% | 5 | 0.04% |
| Arma a 5 stelle | 0.3% | 10 | 0.02% |
| Personaggio a 4 stelle | 2.6% | 18 | 0.14% |
| Arma a 4 stelle | 2.6% | 18 | 0.14% |
| Arma a 3 stelle | 94.3% | 13 | 7.254% |
Utilizzando questi tassi, possiamo quindi determinare quanti lanci sono necessari per raggiungere una certa probabilità cumulativa di aver acquisito un determinato oggetto almeno una volta.
Incorporando i tassi di pietà
Tuttavia, le tariffe di base per gli articoli a quattro e cinque stelle in realtà non raccontano tutta la storia. Tassi di pietà, o Garanzie, possono influenzare notevolmente il calcolo. Essenzialmente, fanno la funzione di probabilità cumulativa discontinuo cambiando la frequenza con cui gli oggetti appaiono periodicamente, fintanto che nessun oggetto del livello specificato è stato evocato dopo un numero sufficiente di tiri. Ci sono diversi modi per compensare questo. Nel gioco, un secondo tasso, chiamato il Tasso medio, comprese le garanzie, viene visualizzato accanto alla tariffa base. Si potrebbe sostituire il tasso di base con questo tasso medio rettificato e i risultati sarebbero più accurati. L'approccio più accurato sarebbe quello di utilizzare il tasso di base, ma segmentare la funzione in base agli intervalli in cui si verificano i tassi di pietà. Tuttavia, questo ha l'indesiderabile risultato di richiedere più calcoli e creare una funzione discontinua. Perde anche un po' di precisione quando si lavora con le probabilità di sottocategoria, poiché una parte dei giocatori che raggiungono la soglia del tasso di pietà avrà già evocato un oggetto dal livello desiderato, facendo riposare il contatore della pietà, ma non l'oggetto desiderato; e non è banale poi aggiungere fasi di pietà discontinue ad ogni successivo tiro per stimare quando il contatore potrebbe essere stato azzerato. Pertanto, una soluzione analitica pura non è possibile: è possibile calcolare solo un limite superiore o inferiore approssimativo in modo analitico.
Il risultato più desiderabile sarebbe una simulazione computazionale completa che potrebbe poi essere confrontata con i vari metodi analitici.
Personaggi degli eventi
Personaggio evento promozionale a 5 stelle
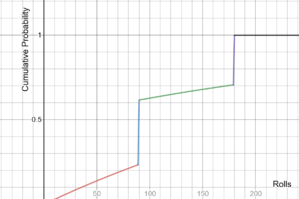
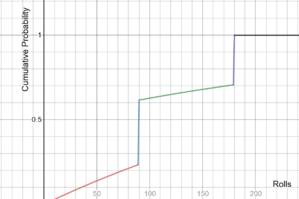
Le possibilità di aver già evocato il personaggio stendardo 5*. Si noti che questa soluzione analitica presuppone che tutti coloro che ricevono un'invocazione di pietà la ricevano alla 90a o alla 180a convocazione, il che potrebbe non essere vero nella pratica.
Per un personaggio evento promozionale a 5 stelle, la percentuale di base è dello 0.3% (tasso di base a cinque stelle diviso per due, poiché c'è una probabilità del 50% di evocare il personaggio dell'evento a 5 stelle ogni volta che si verifica un'evocazione a 5 stelle). C'è anche un meccanismo di pietà in atto, in modo tale che se un'evocazione a 5 stelle non si è verificata entro 89 convocazioni, l'evocazione successiva è garantita come un'evocazione a 5 stelle. Insieme, queste due meccaniche di pietà assicurano che siano necessari al massimo 180 desideri per evocare un personaggio promozionale a 5 stelle. Una soluzione analitica che prescinde dalla prima meccanica della pietà (la garanzia) può essere vista nel grafico seguente.
Il motivo per cui questa soluzione analitica ignora la garanzia è che cambia la velocità con cui si verificano gli eventi (dallo 0.3% delle volte, metà di tutti i pull 5*, allo 0.6% delle volte, il 100% di tutti i pull 5*). Il modo in cui ciò incide sulla velocità con cui si verificano gli eventi nella pratica non è banale: è ovvio che al primo lancio il tasso sarà dello 0.3% per tutti, e che al 90° lancio il tasso sarà dello 0.6% per tutti i giocatori rimasti. Tuttavia, per determinare come cambia la velocità media durante i primi 89 rulli sarebbe necessario risolvere un'equazione differenziale. Tuttavia, possiamo evitarlo del tutto e ottenere un risultato più accurato, effettuando una simulazione.
Come è stato spiegato, la meccanica della pietà rende molto difficile trovare una soluzione analitica significativa al nostro problema. Per ovviare a ciò, possiamo eseguire una simulazione di un gran numero di rulli e analizzare i risultati empiricamente o confrontarli con la nostra soluzione analitica. Poiché il numero restituito dalla funzione di probabilità cumulativa 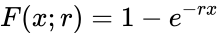 rappresenta la percentuale di una data popolazione che ci aspettiamo di aver sperimentato un risultato almeno una volta dopo
rappresenta la percentuale di una data popolazione che ci aspettiamo di aver sperimentato un risultato almeno una volta dopo 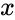 numero di lanci, possiamo simulare i risultati di questa funzione prendendo una grande "popolazione" di individui simulati e rotolando con ciascuno fino a raggiungere il risultato desiderato o il numero massimo di lanci. Quindi aggiungiamo il numero di persone che hanno raggiunto il risultato in un dato passaggio a quelle che hanno già raggiunto il risultato, creando una curva che mostra quando ogni membro della nostra popolazione ha raggiunto il risultato desiderato. Di seguito puoi vedere le rispettive curve di due di queste simulazioni, una con diecimila individui simulati, l'altra con cento.
numero di lanci, possiamo simulare i risultati di questa funzione prendendo una grande "popolazione" di individui simulati e rotolando con ciascuno fino a raggiungere il risultato desiderato o il numero massimo di lanci. Quindi aggiungiamo il numero di persone che hanno raggiunto il risultato in un dato passaggio a quelle che hanno già raggiunto il risultato, creando una curva che mostra quando ogni membro della nostra popolazione ha raggiunto il risultato desiderato. Di seguito puoi vedere le rispettive curve di due di queste simulazioni, una con diecimila individui simulati, l'altra con cento.
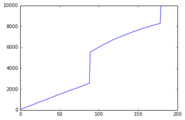
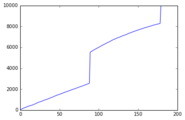 Questa simulazione conteneva 10 "individui". Ognuno ha tirato numeri casuali fino a quando non ha ottenuto il carattere banner 000*, tenendo conto sia della garanzia che il secondo 5* estratto sarà il carattere banner, sia della regola della pietà dei 5 rotoli.
Questa simulazione conteneva 10 "individui". Ognuno ha tirato numeri casuali fino a quando non ha ottenuto il carattere banner 000*, tenendo conto sia della garanzia che il secondo 5* estratto sarà il carattere banner, sia della regola della pietà dei 5 rotoli.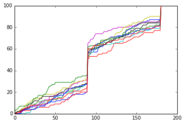
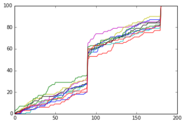 Questo grafico mostra le stesse informazioni, ma per dieci esecuzioni di soli 100 individui simulati. Qui, le curve sono visibilmente frastagliate e ognuna è sostanzialmente diversa dall'ultima, poiché la natura casuale della simulazione non è stata "spalmata" su un numero altrettanto elevato di campioni.
Questo grafico mostra le stesse informazioni, ma per dieci esecuzioni di soli 100 individui simulati. Qui, le curve sono visibilmente frastagliate e ognuna è sostanzialmente diversa dall'ultima, poiché la natura casuale della simulazione non è stata "spalmata" su un numero altrettanto elevato di campioni.
Il grande risultato di queste simulazioni è il seguente:
- La soluzione analitica è il più delle volte sottostimata, mostrando quasi il 30% della popolazione che raggiunge la seconda pietà, mentre le simulazioni mostrano che solo il 20% circa degli individui simulati arriverà fino al 180esimo desiderio/tiro senza avere ricevuto il carattere banner 5* almeno una volta. Questo accade soprattutto perché non teniamo conto della variazione del tasso, dallo 0.3% allo 0.6%.
- La soluzione analitica mostra una porzione più ampia della popolazione che riceve la propria pietà al novantesimo ruolo (vicino al 90%) di quanto effettivamente accada (vicino al 60% nelle simulazioni). Questo è l'unico caso di sovrastima nella soluzione analitica, e succede perché non teniamo conto delle persone che potrebbero aver ricevuto un 55* (ma non il carattere banner) ad un certo punto tra il 5° e il 1° tiro, e quindi non hanno diritto alla pietà al novantesimo tiro. Vedrai, tuttavia, che la curva nelle simulazioni aumenta molto più rapidamente dopo il 90esimo tiro, perché questi individui stanno ricevendo la propria pietà leggermente più tardi di tutti gli altri.
- Anche in un ambiente di simulazione, ci sono ancora grandi picchi al 90esimo e 180esimo desiderio. Questo perché gran parte della popolazione simulata sta attivando il meccanismo della pietà; la pietà, che si attiva dopo 90 desideri infruttuosi, si verifica quando ci aspettiamo che solo il 30% circa della popolazione abbia evocato 5*. Ciò significa che quando un giocatore va fino in fondo alla pietà, non è "sfortunato" se definiamo essere fortunato come raggiungere il risultato desiderato prima del 50% degli altri partecipanti in una data popolazione. Circa i due terzi dei giocatori proveranno sempre pietà. Questo è ciò che rende il Tasso medio, comprese le garanzie, ingannevole. Anche se questo tasso è la media su un gran numero di tiri, se implementi una regola di arresto (un giocatore smette di tirare dopo aver ottenuto l'oggetto desiderato), il tasso effettivo è sempre più basso (perché, a meno che tu non finisca con un tiro di pietà, ci sarà abbi sempre un po' di pietà che tu non abbia raggiunto).
- In particolare, circa il 20% della popolazione non riceverà il carattere banner 5* fino al 180esimo tiro. Ciò significa che se ti impegni a tirare fino a ottenere un certo carattere stendardo, hai una possibilità su cinque di "andare fino in fondo" alla seconda pietà. Allo stesso modo, c'è circa una possibilità su cinque che tiri il personaggio tra i tiri 1 e 89; e dei restanti tre quinti del tempo, tirerai il personaggio o sulla prima pietà, o tra i rulli 91 e 179, divisi quasi equamente.
Personaggio evento promozionale a 4 stelle
Risolvere le densità di probabilità per i caratteri a 4 stelle è, in generale, più complicato dei caratteri a 5 stelle. Questo perché il pool di personaggi è più grande, ci sono sempre armi nel pool e non c'è alcuna garanzia di ottenere un particolare personaggio a 4 stelle. Tuttavia, per risolvere la probabilità cumulativa di ottenere almeno uno dei caratteri evento a 4 stelle, il processo è lo stesso del carattere evento a 5 stelle, ma con percentuali diverse nelle formule. Quindi, queste informazioni sono relativamente facili da ottenere (dobbiamo solo ripetere i passaggi precedenti). Per i personaggi a 4 stelle, è anche più probabile che siamo interessati a quanti di loro è probabile che otteniamo oltre una certa quantità fissa di desideri, di solito 90 o 180; perché, nel contesto dell'ottenimento di un personaggio 5*, sono ricompense bonus. Quindi, esamineremo anche questo problema.
Qualsiasi personaggio evento a 4 stelle
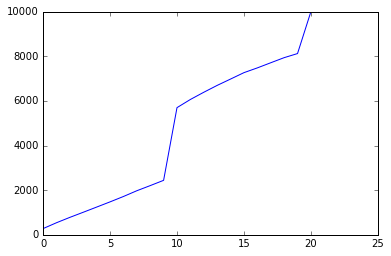
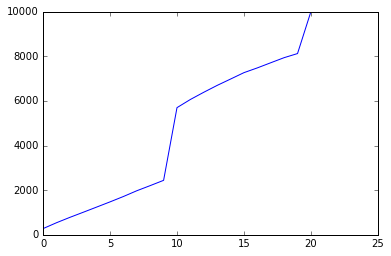
Questa è una simulazione, con n=10, di individui che rotolano sul banner dell'evento che hanno ricevuto almeno un carattere banner 000*.
Se non siamo preoccupati di ottenere un particolare personaggio a 4 stelle, la matematica è molto più semplice. Se siamo interessati a quanti desideri ci vorranno per ottenere almeno un personaggio a 4 stelle, le formule sono le stesse del personaggio a 5 stelle, ma le tariffe sono leggermente diverse. A destra c'è un grafico di una simulazione con 10 individui, con i tassi e il contatore della pietà regolati per riflettere i caratteri a 000 stelle.
Come previsto, la curva è molto simile alla curva per il personaggio dell'evento a 5 stelle, ma su un numero di desideri molto inferiore. I cut-off pietosi si verificano a percentuali di popolazione molto simili, tuttavia, il che non è un risultato banale; ciò indica che i tassi e la pietà sono stati scelti intenzionalmente per tagliare la stessa percentuale prevista della popolazione (circa il 30%) sia per gli elementi a 5 stelle che a 4 stelle.
Un particolare personaggio dell'evento a 4 stelle
Personaggi della voglia di viaggiare
Armi dell'evento
Boss e domini
Proprietà della funzione di probabilità cumulativa
Convergenza indipendente dal tasso
La fortuna e l'errore del giocatore d'azzardo
Relazione con la monetizzazione
- ↑ https://en.web pagepedia.org/web page/Cumulative_distribution_function#Examples
Possibilità cumulativa
(y = 0.5)
90%Possibilità cumulativa
(y = 0.9)
99%Possibilità cumulativa
(y = 0.99)
Grafico dadi a 6 facce 4.16 13.82 27.63
5 curve, una per ogni dado, che mostrano la loro probabilità cumulativa all'aumentare del numero di lanci